publications

2025

1. 

   The Butterfly Effect: Neural Network Training Trajectories Are Highly Sensitive to Initial Conditions

   Gül Sena Altıntaş, Devin Kwok, Colin Raffel, and 1 more author

   In Forty-second International Conference on Machine Learning, 2025

   Abs Bib Open Review PDF Code

   Neural network training is inherently sensitive to initialization and the randomness induced by stochastic gradient descent. However, it is unclear to what extent such effects lead to meaningfully different networks, either in terms of the models’ weights or the underlying functions that were learned. In this work, we show that during the initial “chaotic” phase of training, even extremely small perturbations reliably causes otherwise identical training trajectories to diverge—an effect that diminishes rapidly over training time. We quantify this divergence through (i) L^2 distance between parameters, (ii) the loss barrier when interpolating between networks, (iii) L^2 and barrier between parameters after permutation alignment, and (iv) representational similarity between intermediate activations; revealing how perturbations across different hyperparameter or fine-tuning settings drive training trajectories toward distinct loss minima. Our findings provide insights into neural network training stability, with practical implications for fine-tuning, model merging, and diversity of model ensembles.

   @inproceedings{altintas2025butterfly,
     title = {The Butterfly Effect: Neural Network Training Trajectories Are Highly Sensitive to Initial Conditions},
     author = {Alt{\i}nta{\c{s}}, G{\"u}l Sena and Kwok, Devin and Raffel, Colin and Rolnick, David},
     booktitle = {Forty-second International Conference on Machine Learning},
     year = {2025},
     url = {https://openreview.net/forum?id=L1Bm396P0X},
     open_review = {https://openreview.net/forum?id=L1Bm396P0X},
   }

2024

1. 

   The Butterfly Effect: Tiny Perturbations Cause Neural Network Training to Diverge

   Gül Sena Altıntaş, Devin Kwok, and David Rolnick

   In High-dimensional Learning Dynamics 2024: The Emergence of Structure and Reasoning, 2024

   Abs Bib Open Review PDF

   Neural network training begins with a chaotic phase in which the network is sensitive to small perturbations, such as those caused by stochastic gradient descent (SGD). This sensitivity can cause identically initialized networks to diverge both in parameter space and functional similarity. However, the exact degree to which networks are sensitive to perturbation, and the sensitivity of networks as they transition out of the chaotic phase, is unclear. To address this uncertainty, we apply a controlled perturbation at a single point in training time and measure its effect on otherwise identical training trajectories. We find that both the Ł^2 distance and the loss barrier (increase in loss on the linear path between two networks) for networks trained in this manner increase with perturbation magnitude and how early the perturbation occurs. Finally, we propose a conjecture relating the sensitivity of a network to how easily it is permuted with respect to another network.

   @inproceedings{altintasButterflyEffectTiny2024,
     title = {The {{Butterfly Effect}}: {{Tiny Perturbations Cause Neural Network Training}} to {{Diverge}}},
     shorttitle = {The {{Butterfly Effect}}},
     author = {Alt{\i}nta{\c s}, G{\"u}l Sena and Kwok, Devin and Rolnick, David},
     year = {2024},
     date = {2024-06-16},
     link = {https://openreview.net/forum?id=T1urv73edU&referrer=%5BAuthor%20Console%5D(%2Fgroup%3Fid%3DICML.cc%2F2024%2FWorkshop%2FHiLD%2FAuthors%23your-submissions)},
     urldate = {2024-10-05},
     eventtitle = {High-Dimensional {{Learning Dynamics}} 2024: {{The Emergence}} of {{Structure}} and {{Reasoning}}},
     langid = {english},
     booktitle = {High-dimensional Learning Dynamics 2024: The Emergence of Structure and Reasoning},
     open_review = {https://openreview.net/forum?id=T1urv73edU}
   }

2023

1. 

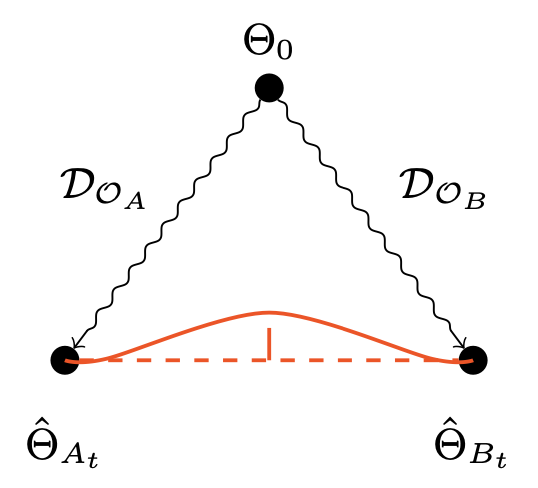   Disentangling Linear Mode Connectivity

   Gül Sena Altıntaş, Gregor Bachmann, Lorenzo Noci, and 1 more author

   In UniReps: Unifying Representations in Neural Models at Neurips 2023, Oct 2023

   Abs arXiv Bib Open Review PDF

   Linear mode-connectivity (LMC) (or lack thereof) is one of the intriguing characteristics of neural network loss landscapes. While empirically well established, it unfortunately still lacks a proper theoretical understanding. Even worse, although empirical data points are abound, a systematic study of when networks exhibit LMC is largely missing in the literature. In this work we aim to close this gap. We explore how LMC is affected by three factors: (1) architecture (sparsity, weight-sharing), (2) training strategy (optimization setup) as well as (3) the underlying dataset. We place particular emphasis on minimal but non-trivial settings, removing as much unnecessary complexity as possible. We believe that our insights can guide future theoretical works on uncovering the inner workings of LMC.

   @inproceedings{altintasDisentanglingLinearMode2023,
     author = {Alt{\i}nta{\c s}, G{\"u}l Sena and Bachmann, Gregor and Noci, Lorenzo and Hofmann, Thomas},
     langid = {english},
     month = oct,
     title = {Disentangling {{Linear Mode Connectivity}}},
     url = {https://neurips.cc/virtual/2023/80398},
     year = {2023},
     open_review = {https://openreview.net/forum?id=2312.09832},
     booktitle = {UniReps: Unifying Representations in Neural Models at Neurips 2023}
   }